Suppose That F is Continuous Function and Integral F2xdx Ap Calc
Integration may be the most challenging concept in AP® Calculus textbooks, but it is also arguably the most important! That being said, there is no shame in being nervous for the upcoming AP® exam. In order to help quell your fears, I will walk you through the most important concepts of solving even the most challenging of integrals. Reading this AP® Calculus review will outline all the tools you need, and hopefully calm the butterflies in your stomach.
Integrals can be split into two separate categories: definite and indefinite. A definite integral has bounds and yields a numerical answer, while an indefinite integral does not have bounds and yields an algebraic answer. Indefinite integrals will be addressed first, since the method for solving them is also used as a part of calculating definite integral solutions.
Indefinite integrals can be solved using two different methods, the anti-chain rule method and the substitution method. Solving an indefinite integral is the same thing as solving for the antiderivative, or undoing the derivative and solving for the original function.
We are now moving on to the fun part: seeing some examples. The anti-chain rule method is basically the reverse of the chain rule method implemented in the derivative section of your textbook. Instead of subtracting one from the exponent, you add one, and instead of multiplying the quantity by the new exponent, you divide it. Let's see an example:
Example 1: Integrate
So we set up the integral, keeping in mind the dx term:
x^3+6x^2-2x.
Next, we integrate each term, adding one to the exponent and dividing the answer by the new exponent value:
\dfrac{1}{4}x^4+2x^3-x^2+c
The c term represents a constant value that is a result of integration and should never be forgotten, especially on multiple choice questions of the AP® Calculus exam.
So far, so good, right? It gets worse. Let's now look at the substitution method, also known as u-substitution. What happens if you are presented with a function that can't be integrated with anti-chain rule? This occurs when multiple functions are multiplied together in ways that cannot be expanded, such as the function in Example 2 below. In this case, we must make a substitution of one of the quantities in order to solve the problem. This is where dx becomes much less like a decorative piece on the end of the integral and much more useful. Let's explain with an example:
Example 2: Integrate 9{\left(x^2+3x+5\right)}^8\left(2x+3\right)
First, as always, set up the integral:
\int{9{\left(x^2+3x+5\right)}^8\left(2x+3\right) dx}
As you can see, chain rule could not be easily applied without expanding the function, which would take a considerable amount of algebra. Let's see if the substitution rule will work. This requires choosing a smart quantity to substitute. I would choose the higher powered function first, but in some cases the choice might not be so clear.
Let u= x^2+3x+5
Since we are changing the function from being in terms of x to being in terms of u, we must solve for du and sub that into the integral function. Never fear! This is simpler than it seems.
If u= x^2+3x+5, then du=2x+3 dx, the derivative of u with respect to x.
We then make these substitutions into the above integral:
\int{9u^8(2x+3)\dfrac{du}{\left(2x+3\right)}}
The (2x+3) term cancels out, and we are left with:
\int{9u^8} du
We can solve this using simple chain rule:
u^9+c
We then sub back in for u with our function in terms of x.
{{(x}^2+3x+5)}^9+c
Now we can clearly see the two main methods for solving indefinite integrals. That wasn't so bad, was it?
Let's take a quick side note to discuss how we treat trig functions in integrals. I'm sure you've tackled trig functions and their identities in your previous math classes. They are extremely important functions, but their integrals are relatively simple. The only method to solving these integrals is to memorize the solution. They were proved by famous mathematicians a long time ago, and in AP® Calculus we don't need to worry about where they came from.
Table 1: The integrals of Trig Functions | |
Function | Integral |
| {sin \left(x\right) } | { -cos \left(x\right) }+c |
| {cos \left(x\right) } | {sin \left(x\right) }+c |
| {{sec \left(x\right) }}^2 | {tan \left(x\right) }+c |
| {sec \left(x\right) }{tan \left(x\right) } | {sec \left(x\right) }+c |
| {{csc \left(x\right) }}^2 | { -cot \left(x\right) }+c |
| {csc \left(x\right) }{cot \left(x\right) } | { -csc \left(x\right) }+c |
Now that we are warmed up in the ways of solving indefinite integrals, we can move on to definite integrals. This discussion will involve some theory, but keep in mind that understanding some of the theory behind calculus will help aid your understanding.
Definite integrals are arguably the most important concept in calculus because they often yield real, hard numbers. From an engineering standpoint, this is ideal. Integral action is applied to many real-life problems such as finding velocity profiles of moving fluids in pipes. The best way to come to terms with definite integrals is to look at them from a graphical standpoint.
A definite integral represents the integral of some function from one point on the axis of a graph, a, to another point, b. We write this as:
\int^{{\mathbf b}}_{{\mathbf a}}{{\mathbf f}\left({\mathbf x}\right){\mathbf dx}}
This integral represents the area under a curve on the graph. This is a complicated concept to understand. The area under the curve could represent anything and normally depends on the concept behind the problem. For AP® Calculus, the concept does not matter, and we just focus on the math; however, there may be concept questions asking what the integral represents, and what's the answer? That's right, the area under the curve. Let's look at an example to make this clear!
Example 3: Set up the integral for integrating the function f\left(x\right)= x^2 from x=-2 to x=2 and graph it.
First, we write the integral in the standard notion:
\int^2_{-2}{x^2dx}
We then graph this function and color in the section that we are interested in from -2 to 2.
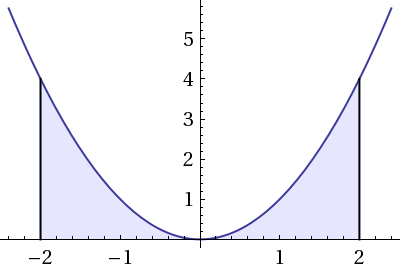
As you can see, only the area that is literally between the function and the x-axis is colored in. When you compute a definite integral, you obtain the value of this area! Pretty neat, right? So how do we solve definite integrals on paper, without graphs? Let's find out!
When computing definite integrals in AP® Calculus, we use the Fundamental Theorem of Calculus. If this name doesn't prove how important integration is in calculus, nothing will. The Fundamental Theorem states that if a function, f(x), is continuous from x=a to x=b, and F(x) is the antiderivative of f(x), then
\int^b_a{f\left(x\right)dx=F\left(b\right)-F(a)}
But what does continuous mean? In order for a function to be continuous, there must be no breaks, jumps, or vertical asymptotes in the function. So how do we solve these problems? The Fundamental Theorem, at first glance, does look like a lot of mumbo-gumbo. Let's walk through an example.
Example 4: Solve this definite integral: \int^2_1{\sqrt{2x+1} dx}
First, we solve the problem as if it is an indefinite integral problem. The chain rule method would not easily apply to this situation so we will use the substitution method. We will let u=2x+1, and therefore, du=2 dx. Let's substitute these values in. The integral now becomes
\int^2_1{\sqrt{u}} \dfrac{du}{2}
Solving the integral as if it were an indefinite integral, we obtain the solution
\dfrac{2}{3}u^{\dfrac{3}{2}}+c
We then substitute in the original function, and our answer becomes
\dfrac{2}{3}{\left(2x+1\right)}^{\dfrac{3}{2}}+c
The next part of the solution is solely based on the Fundamental Theorem. The constant value that is present in all indefinite integral solutions is a representation in the uncertainty of the answer. When we aren't give bounds or initial conditions, we cannot solve for the constant value. When we are solving definite integrals, however, we do have bounds, and a tangible solution can be obtained without the undefined constant. In fact, the answer will have no algebraic parts at all! So in order to incorporate the Fundamental Theorem, we drop the constant term and we plug in to the Theorem equation:
\int^2_1{\sqrt{2x+1} dx}=F\left(2\right)-F(1)
In this case, F\left(x\right)= \dfrac{2}{3}{\left(2x+1\right)}^{\dfrac{3}{2}}, and so we calculate F\left(2\right) and F\left(1\right).
F\left(2\right)= \dfrac{2}{3}{\left(2(2)+1\right)}^{\dfrac{3}{2}}=7.45
F\left(1\right)= \dfrac{2}{3}{\left(2(1)+1\right)}^{\dfrac{3}{2}}=3.46
Therefore,
\int^2_1{\sqrt{2x+1} dx}=7.45-3.46=3.99
As you can see, the answer is purely numerical! Isn't that useful?
There are a few properties of definite integrals that are important to cover in any AP® Calculus review. First, if a function is real and defined at a value of x=a, then:
\int^a_a{f\left(x\right)dx=0}
This is apparent after you look at the Fundamental Theorem and see that F\left(a\right)-F\left(a\right)=0 because they represent the same value.
Second, an integral can be reversed. What does this mean? This means that the bounds of the integral could be switched. The reverse integral would then just be the negative version. In calculus notation:
\int^b_a{f\left(x\right)dx= -\int^a_b{f\left(x\right)dx}}
Third, let's say that our function is continuous and defined at x=a,b, and c on a closed internal. Then, we could say that
\int^c_a{f\left(x\right)dx= \int^b_a{f\left(x\right)dx+ \int^c_b{f\left(x\right)dx}}}
Definite integrals can also be incorporated into other theorems. For instance, the Mean Value Theorem can be adjusted to apply to integrals. Recall from your prior calculus knowledge that the Mean Value Theorem is normally defined as
f'\left(c\right)= \dfrac{f\left(b\right)-f(a)}{b-a}
We know that the Mean Value Theorem applies when f(x) is a continuous and defined function between x=a and b, then we know that there is at least one value of c such that the above equation holds true. When using definite integrals, the equation becomes:
f\left(c\right)= \dfrac{1}{b-a}\int^b_a{f\left(x\right) dx}
This c value is also known as the average value, or the mean value, of a function and it can be calculated given the function and the interval of interest.
Another important theorem that uses definite integrals is the Second Fundamental Theorem of Calculus. Don't you think they could have come up with more creative names for these theorems? Mathematicians are a very blunt group. The Second Fundamental Theorem states that if a function is continuous on the desired interval from x=a to x=b, then the function F\left(x\right)= \int^x_a{f\left(t\right)dt} has a derivative at every point x in the interval and therefore,
F'\left(x\right)= \dfrac{d}{dx}\left(\int^x_a{f\left(t\right)d t}\right)=f\left(x\right)
Logical, right? I know these theorems are not the most exciting part of integration, but they are definitely as important as being able to solve an integral on the AP® Calculus exam!
AP® Calculus practice is one of the best ways to study for the big exam. College Board publishes the free response sections of the old exams online and I encourage you to work as many of the old exams as you can! In all types of math, practice really does make perfect. Here we will work an example free response question to get you started.
Example 5: 1999 AP® Calculus AB Free Response, Question 1
A particle moves along the y-axis with velocity given by v\left(t\right)={rm\quad tsin(}t^2) for tge\quad 0.
1. In which direction (up or down) is the particle moving at time t=1.5? Why?
2. Find the acceleration of the particle at time t=1.5. Is the velocity of the particle increasing? Why or why not?
3. Given that y(t) is the position of the particle at time t and that y\left(0\right)=3, find y(2).
4. Find the total distance traveled by the particle from t=0 to t=2.
First, let's take a step back and observe the framework of the problem. Like all AP® Calculus free response problems, this example has multiple parts that ask for a variety of things. Parts (a) and (b) do not require integration, so we will skip those problems in this exercise.
Part (c) asks for the particles position at a specific time. We know that velocity is the derivative of position, and therefore we will need to integrate the given equation to solve for the velocity profile. Do we use a definite or an indefinite integral? We see that a definite integral would give us the total displacement of the particle. We do not want that. We also see that we are given an initial condition for the particle; therefore, we can use an indefinite integral and solve for the constant value!
Let's begin by setting up the integral:
\int{{rm\quad tsin}\left(t^2\right)dt}
We see that we need to make a substitution in order to solve this problem. Let's make u= t^2 and therefore, du=2dt. Plugging in, we get:
\int{tsin\left(u\right)\dfrac{du}{2t}}
We can cancel the two t's and solve the integral in terms of u:
\int{\dfrac{1}{2}sin\left(u\right)du}= -\dfrac{1}{2}{cos \left(u\right) }+c
We then plug our original substitution back in:
-\dfrac{1}{2}{cos \left(t^2\right) }+c
Now we can solve for c with our initial condition:
-\dfrac{1}{2}{cos \left(0^2\right) }+c=3
0+c=3
c=3
Therefore, our position equation becomes:
y\left(t\right)= -\frac{1}{2}{cos \left(t^2\right) }+3
Solving for when t=2, we get:
y\left(2\right)= -\dfrac{1}{2}{cos \left(2^2\right) }+3=3.527
Part (d) is also an integration problem. The total distance traveled by the particle is another way to ask for the displacement of the particle from t=0 to t=2. We therefore know that we need to use a definite integral. We also know that the first step of solving an integral is solving for the indefinite integral equation, which we have already done in part (c). Therefore, we can skip to using the Fundamental Theorem of Calculus:
\int^2_0{tsin\left(t^2\right)dt}=y\left(2\right)-y(0)
We realize that we have already calculated both of these values! Therefore, we just plug in and solve:
Displacement = y\left(2\right)-y\left(0\right) = 3.527 – 3 = 0.527
Eureka! The AP® Calculus exam is often filled with little shortcuts like this because the exam is timed. Be sure to watch out for them so that you can finish the exam!
As we have seen, integration is not so bad. You now have all the tools to master the AP® Calculus exam! Keep in mind, however, that practice makes perfect! Do you think we have left something out? Let us know! Applications for integration are covered in other articles!
Looking for AP® Calculus practice?
Check out our other articles on AP® Calculus.
You can also find thousands of practice questions on Albert.io. Albert.io lets you customize your learning experience to target practice where you need the most help. We'll give you challenging practice questions to help you achieve mastery of AP® Calculus.
Start practicing here .
Are you a teacher or administrator interested in boosting AP® Calculus student outcomes?
Learn more about our school licenses here.
Source: https://www.albert.io/blog/how-to-solve-integrals-ap-calculus-crash-course/
0 Response to "Suppose That F is Continuous Function and Integral F2xdx Ap Calc"
Post a Comment